Research
DFG Project (2025-2028)

Simulation and Numerical Analysis of Multicomponent Bose–Einstein Condensates
PI: Prof. Dr. Daniel Peterseim, Prof. Dr. Tatjana Stykel
Multicomponent Bose-Einstein condensates (BECs) represent a frontier research area in atomic and condensed matter physics. Given the challenges of observing these systems experimentally, numerical simulation plays a crucial role in studying their behaviour. However, the multiple interacting species and spin degrees of freedom in multicomponent BECs pose fundamental theoretical and computational challenges. Existing numerical methods, designed primarily for single-component systems, cannot fully capture the complexity of multicomponent condensates, in particular the intricate interplay of spin interactions, rotational dynamics and strong nonlinearities. Furthermore, these methods lack the efficiency required for large-scale simulations and the theoretical guarantees needed to ensure convergence and stability in extreme parameter regimes.
This proposal aims to fill this gap by developing and rigorously analysing advanced numerical methods for the coupled Gross-Pitaevskii equations governing multicomponent BECs. First, we will introduce novel Riemannian optimisation methods for ground state computations, formulating the problem on infinite-dimensional manifolds equipped with energy-adaptive metrics to ensure reliable convergence and to prevent significant dependence on the type and resolution of the spatial discretisation. Second, we will design structure-preserving spatial discretisation schemes that preserve key physical properties such as positivity, uniqueness and stability, while eliminating non-physical artefacts. Finally, we will develop conservative time integration algorithms that preserve crucial invariants such as energy, mass and magnetisation, allowing accurate simulation of nonlinear dynamical phenomena.
Altogether, by providing a robust computational framework tailored to the complex physics of multicomponent BECs, this project will enable the numerical exploration of ground states of multicomponent BECs and their dynamics, focussing on challenging effects of spinor interactions and rotating frames. Beyond the specific application, the mathematical and algorithmic innovations in Riemannian optimisation and structure-preserving numerical methods are expected to impact broader classes of nonlinear Schrödinger equations and associated nonlinear eigenvalue problems.
Project within DFG Priority Program 2256 (2023-2026)
Novel Approaches for the Multidimensional Convexification of Inelastic Variational Models for Fracture
PI: Prof. Dr. Daniel Peterseim
Damage modelling and simulation is of fundamental engineering interest. At the macroscale, damage manifests itself through stress- and strain-softening effects as well as fracture in terms of the formation and propagation of cracks. When reaching certain degrees of microscopic damage, classical continuum damage models encounter a loss of convexity of the associated incremental variational formulation, which limits their usefulness fundamentally.
Relaxation approaches based on convexification lead to models that provide mesh-independent solutions and often describe homogenised microstructures. Although significant steps forward with respect to efficient numerical convexification schemes have recently been made, computations for complex engineering structures in three dimensions are infeasible as of today. Hence, one of the main goals in this research project is to exploit offline- and online (machine) learning strategies to enable relevant computational simulations using relaxed damage models. Moreover, novel convexification approaches based on PDE formulations or polyconvexification rather than approximating the rank-one convex envelope constitute promising alternatives for relaxed models, which are to be developed with improved efficiency. The speed-up to be expected from these approaches will be necessary for more complex mechanical problems including brittle and ductile fracture in the sense of macroscopic crack propagation, where learning strategies alone may become more expensive. Therefore, the final major aim of this research project is to extend the incremental variational formulations to capture plastic effects combined with damage for brittle and ductile fracture-related problems.
Project partner: Prof. Dr. Malte A. Peter (Universität Augsburg)
Project partner: Prof. Dr.-Ing. habil. Daniel Balzani (Ruhr Universität Bochum)
DFG Project (2022-2025)

Autonomous research for exploring structure-property linkages and optimizing microstructures
PI: Prof. Dr. Daniel Peterseim
Developing novel materials plays an important role in technological innovations. Especially the relationship between the process parameters, the local material structure and the resulting properties is of great interest. Since the local structure of the materials essentially dictates its properties, the generation and understanding of structure-property (SP) linkages is of utmost importance. The envisioned project aims to establish reliable SP linkages fast and cheaply, thereby identifying realistic, manufacturable material structures with optimal properties.
The experimental exploration of SP linkages requires considerable technological effort. The achievable limited data basis is a major obstacle for the application of modern machine learning methods. To this end, model-based numerical simulations can provide a remedy in the form of synthetic data. Furthermore, a practically relevant algorithm requires the automated generation of synthetic microstructures and numerical simulations on selected samples in order to systematically extend the experimental data base. This procedure, referred to as autonomous research, is developed and implemented in a material-independent manner and validated using two exemplary microstructures. Altogether, the synthesis of model-based numerical simulation and data-driven algorithms promises to provide a deeper understanding of the mechanisms of action underlying SP linkages, as well as to accelerate materials development.
Project partner: Prof. Dr.-Ing. habil. Markus Kästner (TU Dresden)
DFG Project (2021-2024)

Decoupling Integration Schemes of Higher Order for Poroelastic Networks
PI: Dr. Robert Altmann
Poroelastic multiple-network models arise in a variety of different application domains, including geoscience and biomedicine. The corresponding system is a coupled partial differential equation of elliptic and parabolic type that, in particular in the 3-dimensional case, is computationally challenging or even unfeasible if standard methods are applied. This project aims to construct a novel class of highly efficient integration schemes of higher order that combine the simplicity of monolithic approaches with the tremendous speed-ups of iterative methods that decouple the problem. Since the spatial discretization of the coupled PDE results in a differential-algebraic equation (DAE), the convergence analysis renders a challenging task. The convergence analysis is based on the fact that the semi-explicit scheme can be interpreted as an implicit scheme for a related delay equation, where the time-delay equals the step size.
Project partner: Dr. Benjamin Unger (U Stuttgart)
DFG Project (2021-2024)
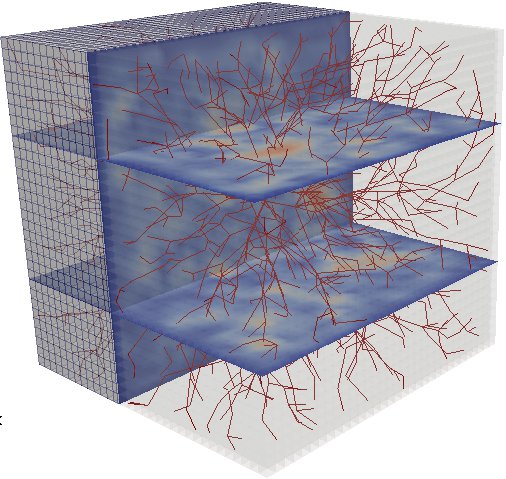

Computational Multiscale Methods for Inverse Estimation of Effective Properties of Poroelastic Tissues
PI: Prof. Dr. Daniel Peterseim
Portal hypertension is a vascular liver disease characterized by a pathologically increased pressure gradient within the blood vessels irrigating and draining the liver tissue. In current clinical practice, the diagnosis of portal hypertension is strongly limited by the necessary invasive catheterization of the hepatic vein. The project aims to foster the development of an alternative, non-invasive technique based on magnetic resonance elastography (MRE), a medical imaging technique sensitive to effective mechanical properties of living tissue. Recent experimental studies demonstrated the potential of MRE for the early and noninvasive detection of such pressure-related diseases. By the development of computational multiscale models of liver tissues, this project aims to develop efficient algorithms for the solution of the inverse problems arising in the context of liver elastography, hence, supporting clinicians towards a non-invasive diagnosis of portal hypertension.
Project partner: Dr. Alfonso Caiazzo (WIAS Berlin)
External partner: Charite-Universitätsmedizin Berlin/Universitätsklinikum Augsburg
Project within DFG Priority Program 2256 (2020-2023)
Convexified Variational Formulations at Finite Strains based on Homogenised Damaged Microstructures
PI: Prof. Dr. Daniel Peterseim
Many soft materials such as elastomers, reinforced polymers, and soft biological tissues show anisotropic softening effects when subjected to large strains. Apart from a complex stress-strain hysteresis under cyclic loading associated with stress-softening, significant strain-softening in the sense of decreasing stresses with increasing strains is essential in the context of currently relevant problems in material design. Striking examples are the delamination or fibre pull-out in reinforced materials. The softening effects originate from a nucleation and evolution of cavities at the microscale, which form damaged microstructures. The resulting behaviour at the macroscale can appropriately be described by classical continuum damage mechanics models, where the microscopic damage is phenomenologically captured by internal variables, which account for the reduced cross-sections in the material. However, when reaching certain degrees of microscopic damage, these models encounter a loss of convexity of the associated incremental variational formulation, which marks a fundamental problem for their usefulness, in particular with respect to their numerical evaluation.
This research project focuses on the design and implementation of novel convexified incremental variational formulations, which are a priori numerically stable. The convexifications will take advantage of homogenised mathematical descriptions of the damage phenomena acting at the microscale. The convexification process allows for a direct interpretation in terms of an evolution of the microstructural damage and the models are automatically well-behaved numerically, e.g. they admit mesh-independent solutions. The main goal is the incorporation of strain-softening effects in the variational damage model.
Project partner: Prof. Dr. Malte A. Peter (Universität Augsburg)
Project partner: Prof. Dr.-Ing. habil. Daniel Balzani (Ruhr Universität Bochum)
ERC Consolidator Grant (2020-2025)
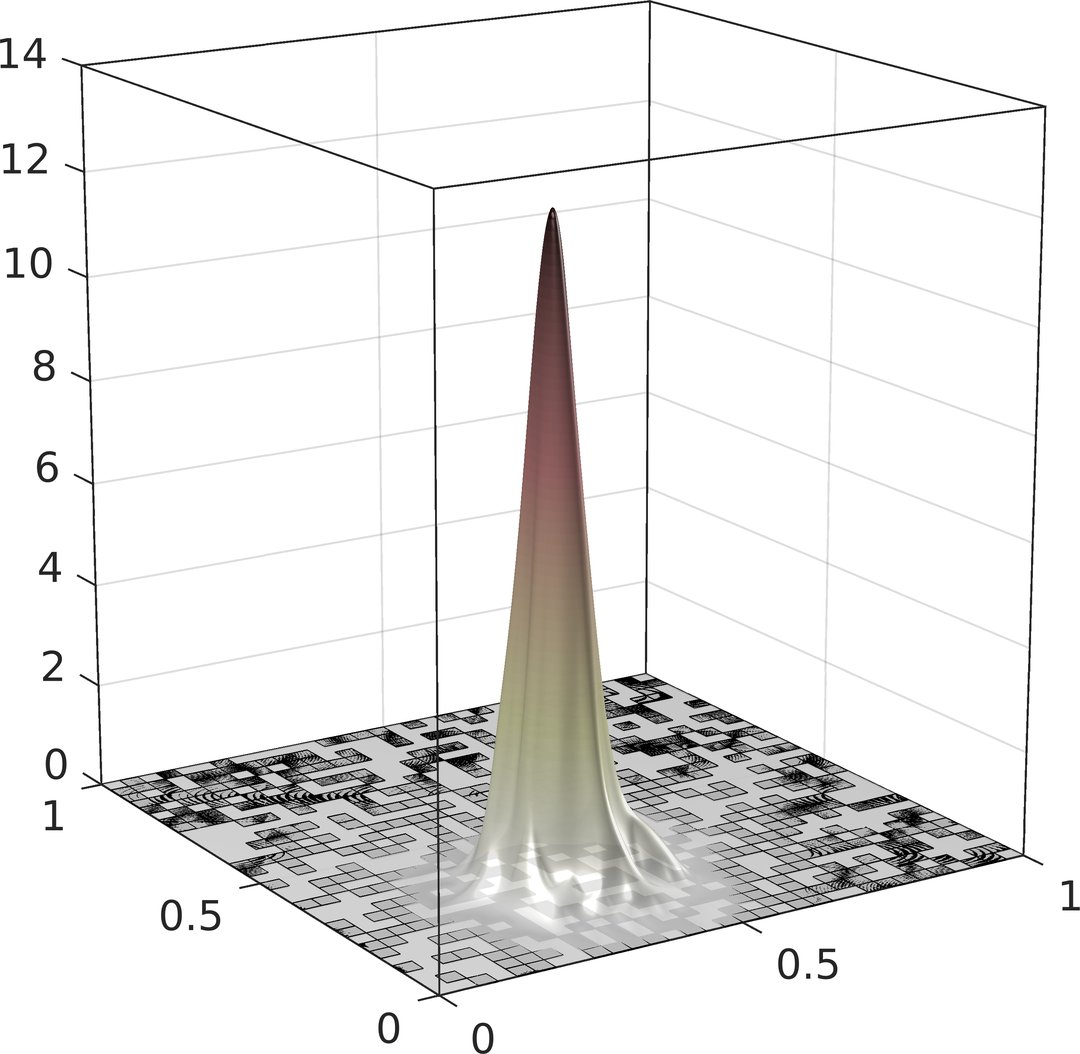
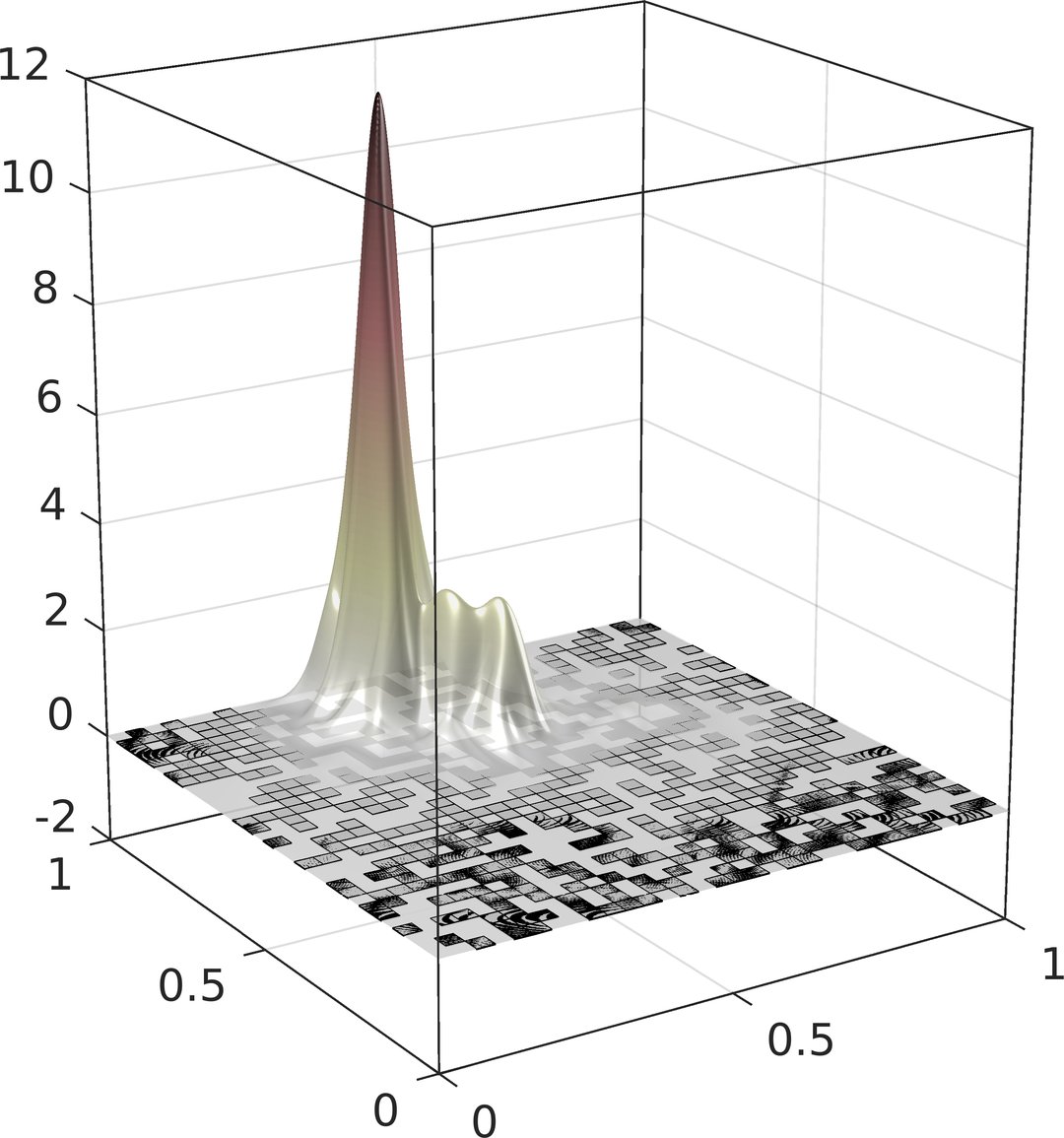
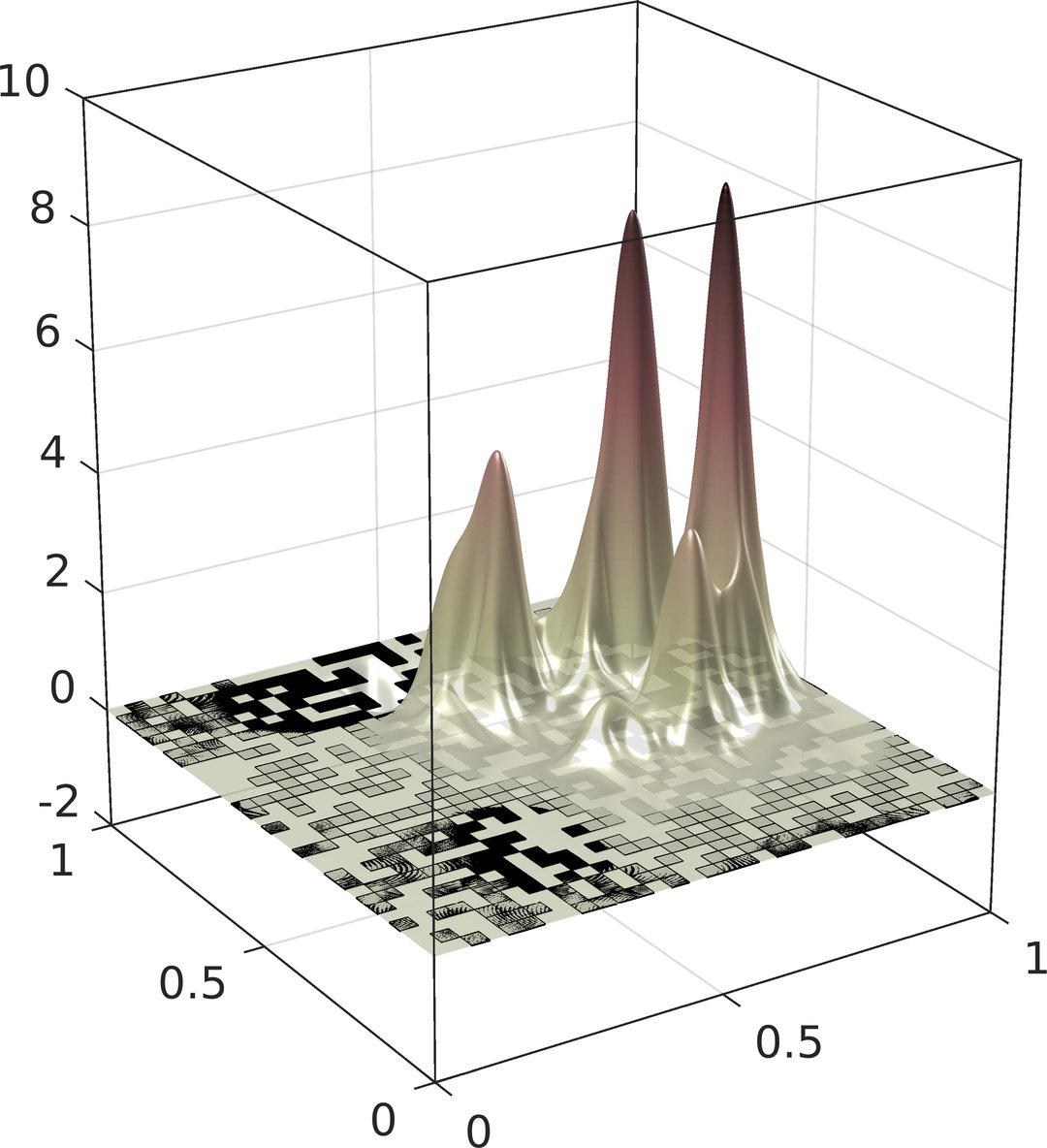

Computational Random Multiscale Problems
PI: Prof. Dr. Daniel Peterseim
Geometrically or statistically heterogeneous microstructures and high physical contrast are the key to astonishing physical phenomena such as invisibility cloaking with metamaterials or the localization of quantum waves in disordered media. Due to the complex experimental observation of such processes, numerical simulation has very high potential for their understanding and control. However, the underlying mathematical models of random partial differential equations are characterized by a complex interplay of effects on many non-separable or even a continuum of characteristic scales. The attempt to resolve them in a direct numerical simulation easily exceeds today's computing resources by multiple orders of magnitude. The simulation of physical phenomena from multiscale models, hence, requires a new generation of computational multiscale methods that accounts for randomness and disorder in a hierarchical and adaptive fashion.
This project concerns the design and numerical analysis of such methods. The main goals are connected to fundamental mathematical and algorithmic challenges at the intersection of multiscale modeling and simulation, uncertainty quantification and computational physics:
(A) Numerical stochastic homogenization beyond stationarity and ergodicity,
(B) Uncertainty quantification in truly high-dimensional parameter space,
(C) Computational multiscale scattering in random heterogeneous media,
(D) Numerical prediction of Anderson localization and quantum phase transitions.
These objectives base upon recent breakthroughs of deterministic numerical homogenization beyond periodicity and scale separation and its deep links to seemingly unrelated theories ranging all the way from domain decomposition to information games and their Bayesian interpretation. It is this surprising nexus of classical and probabilistic numerics that clears the way to the envisioned new computational paradigm for multiscale problems at randomness and disorder.
Community Research and Development Information Service (CORDIS) of the European Commission
DFG Project 446856041 (2020-2023)

Decoupled computational methods for nonlinear parabolic problems with dynamic boundary conditions
PI: Dr. Robert Altmann
Problems with dynamic boundary conditions appear in applications where one needs to reflect the effective properties on the surface. A representative example is the model of a heat source on the boundary of the computational domain. The basis of the project is an alternative formulation of the problem as a partial differential-algebraic equation (PDAE), which considers the bulk and surface dynamics as a coupled system. For this, an additional Lagrange multiplier is inserted to the system equations. Given the PDAE formulation, we aim to construct new approximation schemes, which are robust in terms of the underlying saddle point structure. Thus, we need to consider mixed finite element schemes in combination with techniques known from the field of differential-algebraic equations. In contrast to the standard formulation of the problem, we do not include the bulk-surface coupling into the ansatz space but as an additional constraint on the dynamics. This formal decoupling offers a great flexibility for the spatial discretization, since finite element meshes in the bulk and on the boundary can be chosen independently. This is advantageous, especially if the system contains different characteristic scales or inhomogeneities. The second goal of the project is to construct efficient splitting methods for these PDAE systems in order to deal with appearing nonlinearities.
Project within DFG Priority Program 1748 (2015-2021)




Adaptive isogeometric modeling of discontinuities in complex-shaped heterogeneous solids
PI: Prof. Dr. Daniel Peterseim
The development of innovative products demands multi-material lightweight designs with complex heterogeneous local material structures. Their computer-aided engineering relies on the constitutive modeling and, in particular, the numerical simulation of propagating cracks. The underlying numerical techniques have to account for the failure of interfaces and bulk material as well as their interaction in the form of crack branching and coalescence. In order to provide realistic predictions by simulation, the true 3D nature of the problem has to be captured. For this purpose, this project develops new numerical models and methods that combine adaptive spline-based approximations from Isogeometric Analysis (IGA) with phase-field models for crack propagation. The main goals of this project are linked to fundamental challenges in the fields of Computational Mechanics, Numerical Analysis and Material Sciences, e.g., the representation and adaptive refinement of unstructured (water-tight) spline surfaces, the feasible coupling of spline surfaces with structured bulk meshes, the regularized modeling of heterogeneous materials, and the rigorous error analysis and control in pre-asymptotic regimes.
Project partner: Prof. Dr.-Ing. habil. Markus Kästner (TU Dresden)


